前回の記事では、負の数を学習しました。

\(0\)より小さい数は、\(−\)(マイナス)をつけて表されるのだった!
今回は、加法・減法(足し算・引き算)について学習していきましょう。
足し算(加法)
前回の記事では、数直線上を「前進」または「後退」する人にたとえて正負の数を説明しました。
ここで「足し算」とは、数直線上の人に「前を向け」と指示することといえます。
正の数を足す
いくつかの例を使って考えてみましょう。
例1
\begin{align}
(+2)+(+3)&=+(2+3)\\
&=+5
\end{align}
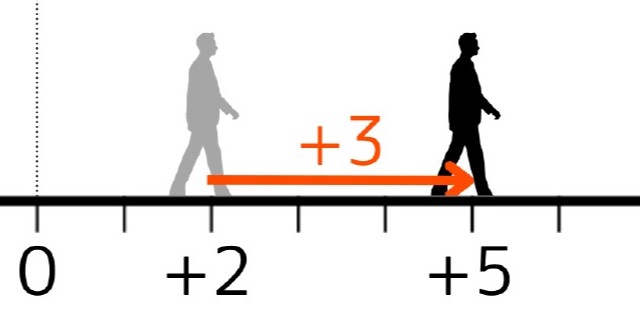
この式は「はじめに+2の位置にいた人が前を向いて3歩前進した。」と翻訳できます。
例2
\begin{align}
(-2)+(+5)&=+(5-2)\\
&=+3
\end{align}
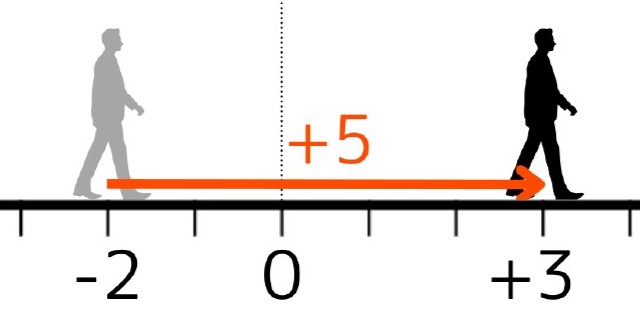
この式は「はじめに-2の位置にいた人が前を向いて5歩前進した。その際、はじめの2歩で0まで戻り、残りの\(5-2=3\)歩でさらに前進した。」と翻訳できます。
例3
\begin{align}
(-5)+(+3)&=-(5-3)\\
&=-2
\end{align}
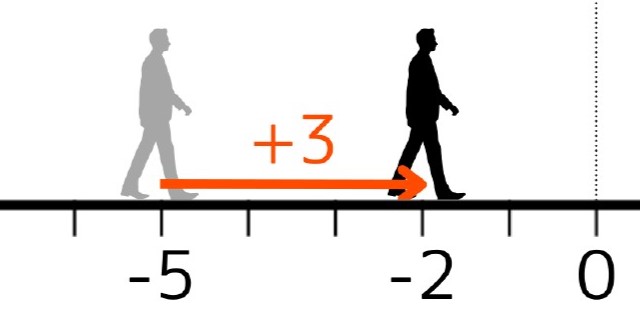
この式は「はじめに-5の位置にいた人が前を向いて3歩前進した。0までは\(5-3=2\)歩足りなかった。」と翻訳できます。
負の数を足す
例4
\begin{align}
(+3)+(-3)&=3-3\\
&=0
\end{align}
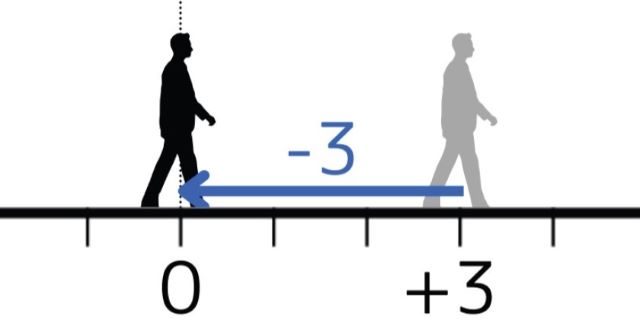
この式は「はじめに+3の位置にいた人が前を向いて3歩後退した。」と翻訳できます。
例5
\begin{align}
(+2)+(-6)&=-(6-2)\\
&=-4
\end{align}
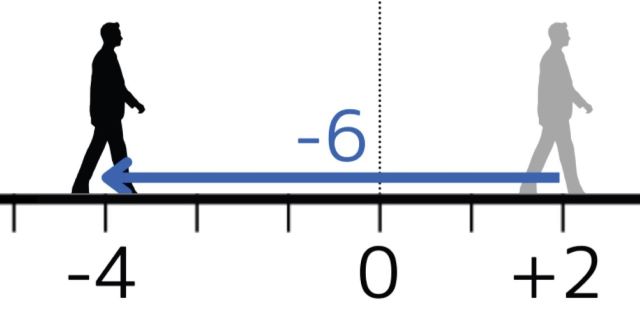
この式は「はじめに+2の位置にいた人が前を向いて6歩後退した。その際、はじめの2歩で0まで戻り、残りの\(5-2=3\)歩でさらに後退した。」と翻訳できます。
引き算(減法)
一方で「引き算」とは、数直線上の人に「後ろを向け」と指示することといえます。
正の数を引く
例6
\begin{align}
(+5)-(+4)&=(+5)+(-4)\\
&=+1
\end{align}
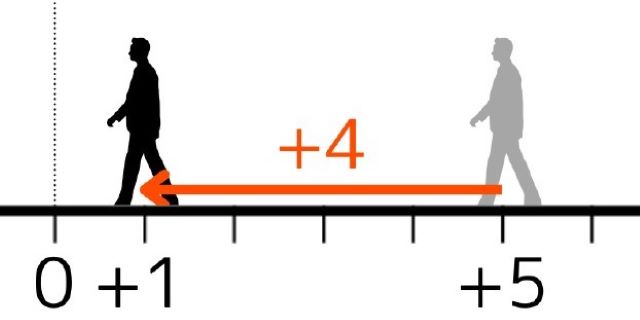
この式は「はじめに+5の位置にいた人が後ろを向いて4歩前進した。」と翻訳できます。
図のように、後ろを向いて前に歩くと、後ろ(負の方向)に進みます。
正の数を引くことは、負の数を足すことに置きかえられるのです。
例7
\begin{align}
(+3)-(+5)&=(+5)+(-3)\\
&=+(5-3)\\
&=-2
\end{align}
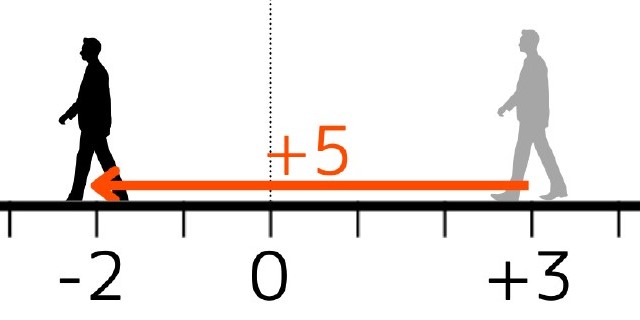
この式は「はじめに+3の位置にいた人が後ろを向いて5歩前進した。その際、はじめの3歩で0まで戻り、残りの\(5-3=2\)歩でさらに前進した。」と翻訳できます。
負の数を引く
例8
\begin{align}
(+1)-(-3)&=(+1)+(+3)\\
&=+1
\end{align}
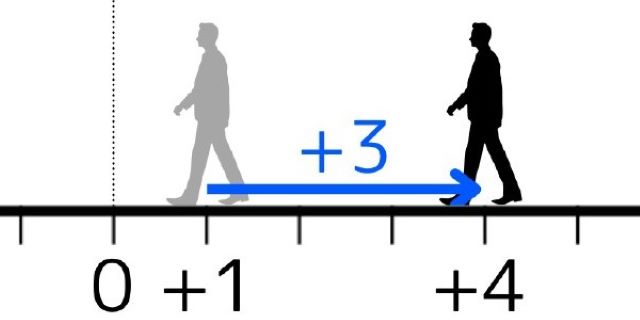
この式は「はじめに+1の位置にいた人が後ろを向いて4歩後退した。」と翻訳できます。
図のように、後ろを向いて後ろに歩くと、前(正の方向)に進みます。
負の数を引くことは、正の数を足すことに置きかえられるのです。
例9
\begin{align}
(-5)-(-4)&=(-5)+(+4)\\
&=-(5-1)\\
&=-1
\end{align}
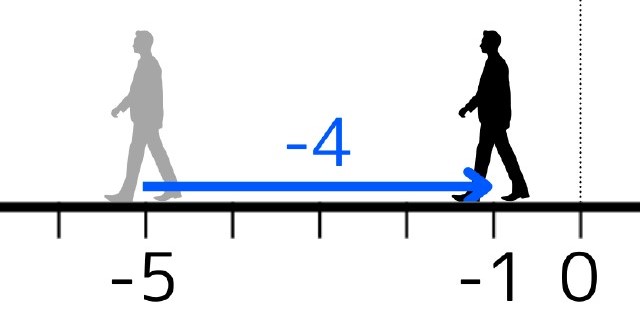
この式は「はじめに-5の位置にいた人が後ろを向いて4歩後退した。0までは\(5-4=1\)歩足りなかった。」と翻訳できます。
ここまでの整理
以上の計算をルールとしてまとめてみましょう。
- 同符号の足し算(プラス(\(+\))とプラス(\(+\))またはマイナス(\(-\))とマイナス(\(-\))の足し算)\(\rightarrow\)「絶対値の和に、共通の符号をつける」
- 異符号の足し算(プラス(\(+\))とマイナス(\(-\))の足し算)\(\rightarrow\)「絶対値の差に、絶対値の大きい方の符号をつける」
- 引き算\(\rightarrow\)「足し算に直してから計算する」
括弧()の省略
ここまで、式には全て括弧()を付けて表してきました。
しかし、毎回括弧を書いていると手が疲れてしまいます。
実際に計算式を書くときは、括弧を省略することがほとんどです。
先頭の数字
式の先頭に来る数字が正の数のときは何もつけず、負の数のときは\(-\)だけを付けます。
例10
\begin{align}
(+3)+(+4) &= 3 + (+4)\\
(-2)-(-5) &= -2 – (-5)\\
(+7)+(-11)&= 7 +(-11)\\
(-8)-(+9)&= -8-(+9)
\end{align}
答えを書くときも、式の先頭と考えて括弧やプラス(\(+\))を省略します。
例11
\begin{align}
3 + (+4) &= 7\\
7 + (-11) &= -4
\end{align}
同符号の場合
同符号が続く場所は「プラス(\(+\))」で置き換えます。
例12
\begin{align}
3+(+4) &= 3 + 4\\
-2-(-5) &= -2 + 5\\
\end{align}
異符号の場合
異符号が続く場所は「マイナス(\(-\))」で置き換えます。
例13
\begin{align}
7+(-11)&= 7 -11\\
-8-(+9)&= -8-9
\end{align}
よくあるまちがい
次のような間違いをした答案をよく見かけます。
\begin{align}
-6-4&= -(6-4)\\
&=-2
\end{align}
\(-6-4\)は、\((-6)+(-4)\)の括弧を省略した書き方ですから、正しくは
\begin{align}
-6-4&= -(6+4)\\
&=-10
\end{align}
となります。
計算に不慣れなうちは、省略前の式の形を想像しながら計算しましょう。
まとめ
改めて、括弧の省略規則をまとめてみましょう。
- 先頭の数字\(\rightarrow\)「マイナス(\(-\))」だけ残す
- 同符号が続く場所\(\rightarrow\)「プラス(\(+\))」で置き換え
- 異符号が続く場所\(\rightarrow\)「マイナス(\(-\))」で置き換え
おわりに
「加法と減法」、特に「負の数の引き算」は中学数学最初にして最大の難所といえます。
ここを乗り越えれば後が楽になると思って、たくさん計算練習をしていきましょう!


