前回は、「文字を使った式」の表し方を学習しました。
今回の記事では、実際に文字式を計算していきましょう!
文字式どうしの足し算
次のような例を考えてみましょう。
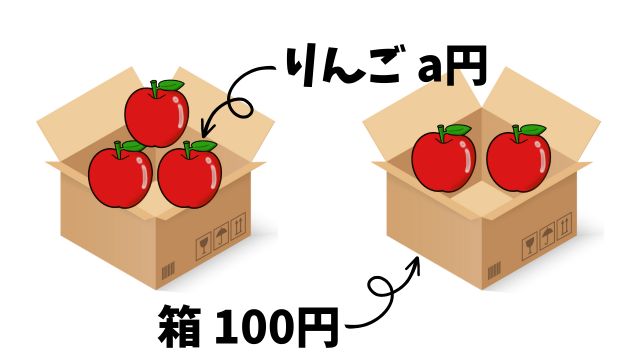
このとき、\(2\)箱の合計金額はいくらになるでしょうか。
計算式の表し方
左の箱には、\(a\)円のりんごが\(3\)つ入っているので、箱(\(100\)円)を含めた合計金額は
\((3a+100)\)円
と表されます。
一方、右の箱にはりんごが\(2\)つ入っているので、箱を含めた合計金額は
\((2a+100)\)円
と表されます。
したがって、\(2\)箱を合わせた金額の計算式は
\[(3a+100)+(2a + 100)\]
と書くことが出来ます。
計算方法
さて、この文字式を計算してみましょう。
合計金額の計算式である\((3a+100)+(2a+100)\)を、「りんごの部分」と「箱の部分」に分けて
\[(3a+100)+(2a+100) = (3a+2a)+(100+100)\]
とすることができます。

ここで、\(3a+2a\)とは、「\(a\)円のりんご\(3\)個と、\(a\)円のりんご\(2\)個を足し合わせる」という意味です。
すなわち、「\(a\)円のりんごが\(5\)個ある」ことになります。
したがって、\(3a+2a=5a\)円です。
また、箱の金額は\(100+100=200\)円となります。
以上より、
\begin{align}(3a+100)+(2a+100) &= (3a+2a)+(100+100)\\ &= 5a + 200\end{align}
と計算することが出来ます。
文字式の計算では、同じ文字どうし・数字どうしを足し引きする
文字式どうしの引き算
次のような例を考えてみましょう。
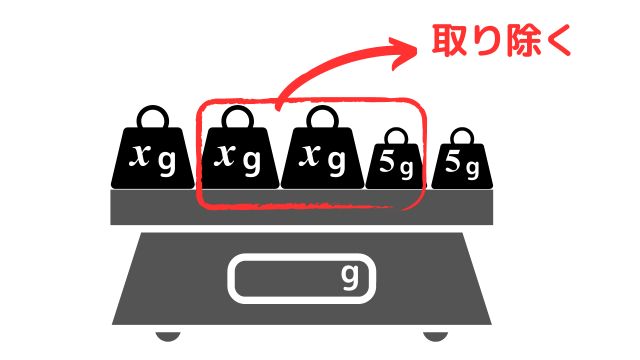
電子天びんに\(x{\rm g}\)のおもりが\(3\)個と\(5{\rm g}\)のおもりが\(2\)個乗っています。
この状態から、\(x{\rm g}\)のおもりを\(2\)個と\(5{\rm g}\)のおもりを\(1\)個取り除きます。
電子天びんの上に残ったおもりの重さは何\({\rm g}\)でしょうか。
計算式の表し方
はじめに乗っているおもりの重さは、\((3x+10){\rm g}\)と表されます。
取り除くおもりの重さは\((2x+5){\rm g}\)と表されます。
したがって、残ったおもりの重さを計算する式は
\[(3x+10)-(2x+5)\]
と書くことができます。
計算方法
「\((2x+5){\rm g}\)のおもりを取り除く」とき、
- \((2x+5){\rm g}\)のおもりを一気に取り除く
- まず\(2x{\rm g}\)のおもりを取り除き、次に\(5{\rm g}\)のおもりを取り除く
という2通りの方法があります。(もちろん、どちらの方法でも結果は同じです)
これを踏まえて、計算式を
\[(3x+10)\color{red}{-(2x+5)}= 3x + 10\color{red}{-2x-5}\]
のようにすることができます。
あとは、同じ文字どうし・数字どうしを計算することで
\begin{align}(3x+10)-(2x+5)&=3x+10-2x-5\\ &= (3x -2x)+(10-5)\\ &= x + 5\end{align}
と答えを求められます。
「一気に引く」ことは、「順番に引く」ことと同じ
様々な例
次の場合はどう計算すればよいでしょうか。
【問題】\((11x+7)-(5x-6)\)を計算しなさい。
「一気に引く」ことは、「順番に引く」ことと同じですから、先ほどの例と同様に
\[(11x+7)\color{red}{-(5x-6)}=11x+7\color{red}{-5x – (-6)}\]
とカッコをはずすことができます。
「\(-6\)を引く」とは、「\(6\)を足す」ことと同じですから、結局
\begin{align}(11x+7)-(5x-6) &= 11x + 7 -5x -(-6)\\ &= 11x + 7 -5x + 6\\&= (11x – 5x) + (7 + 6)\\ &= 6x +13 \end{align}
と答えを求められます。
分配法則を利用した計算
はじめの例に戻って考えてみましょう。

上の例で、りんごと箱の合計金額は\[(3a+100)+(2a+100) = 5a +200\]と計算できることを説明しました。
では、次の場合の合計金額はどう計算できるでしょうか。

これは、はじめの例と同様に、
\[(3a+100)+(2a+100)+(2a+100)\]
と表せます。
さらに、「右の2つの箱の中身は同じである」ことに注目すれば、
\[(3a+100)\color{red}{+2}(2a+100)\]
とも表すことができます。
分配法則とは?
先ほどの式の\(2(2a+100)\)の部分を考えてみましょう。
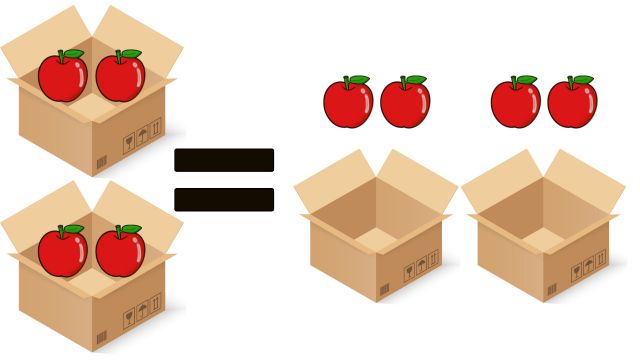
「\((2a+100)\)円を\(2\)回足す」ことは、「まず\(2a\)円を\(2\)回足し、次に\(100\)円を\(2\)回足す」ことと同じですから、
\(\color{red}{2}(2a+100)=\color{red}{2\times}2a + \color{red}{ 2 \times}100= 4a + 200\)
と計算することができます。
上記の考え方による計算方法を、分配法則とよびます。
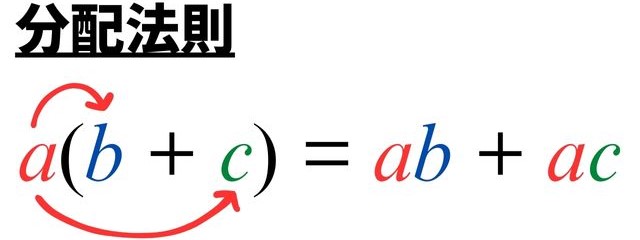
意味:「まとめてかけ算」しても、「個々にかけ算」しても、結果は同じ!
様々な例
次の場合はどう計算すればよいでしょうか。
【問題】\((7x+15)-5(-5x+2)\)を計算しなさい。
式中の省略されている符号(\(+\)や\(\times\))を明示すると、分配法則をどう使えばよいか分かりやすくなります。
答えは、
\begin{align}(7x+15)-5(-5x+2) &= (7x+15)+ (-5)\times(-5x+2)\\ &= 7x + 15 + (-5)\times (-5x) + (-5)\times 2 \\ &= 7x + 15 + 25x -10 \\ &= 32x +5\end{align}
となります。
まとめ
今回は、文字式の計算について解説しました。
文字式の計算において、「分配法則」は強力な考え方の一つとなるので、たくさん練習して習得していきましょう!


