突然ですが、素数に「1」が含まれないのはどうしてか、皆さんは知っていますか?

数学の決まりとして,1は素数ではありません。
出典:https://hiroba.benesse.ne.jp/faq/show/316?site_domain=manabi
確かにその通りです。その通りなのですけど…
「別に1を素数と定義してもいいじゃないか!」とも思ってしまいますよね。
今回はそんな「素数の定義」について、基本的な知識から復習をしていきましょう。
そもそも「素数」とは?
素数とは、「1とその数以外に約数を持たない自然数」のことです。
言いかえれば、「1と自分自身以外で割り切れない自然数」といえます。
例えば、\(7\)の約数は\(1,7\)(\(1,7\)でしか割り切れない)ですから、\(7\)は素数です。
\(15\)の約数は\(1,3,5,15\)(\(1,15\)以外にも\(3,5\)で割り切れる)となるため、\(15\)は素数ではありません。
【問題】次のうち、素数を全て選びましょう。
\(2,5,8,35,47,57\)
(答え)\(2,5,47\)
\(8\div2=4,\;35\div5=7,\;57\div3=19\)より、\(9,21,57\)は素数ではありません。
「素因数分解」について学ぶ
素因数分解とは、「自然数を素数だけの積で表すこと」です。
例えば、\(30=2\times 3\times 5\)のように表すことが出来ます。
同様に、\(20=2\times 2 \times 5 = 2^2 \times 5\)となります。
【注意】同じ数を複数回かける場合、以下のように表します。
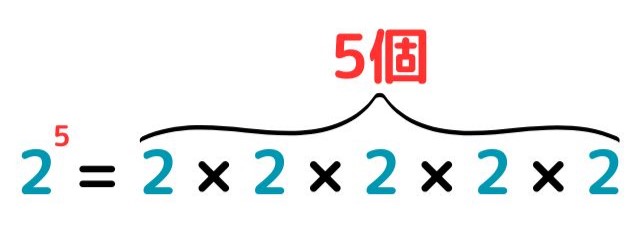
素因数分解をするときは、下のように「割り算の筆算を上下逆向きに書き連ねる」とよいです。
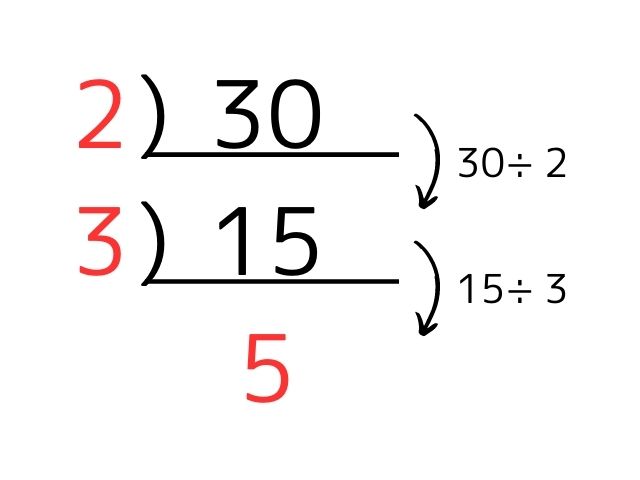
これは、\(30\div 2=15\)と\(15\div 3=5\)の筆算を上下逆向きにして書き連ねたものとなっています。
ここで、赤文字部分(わる数と最後に出てきた商)を見ると、素因数分解の形になっていることが分かります。
【問題】次の数を素因数分解しましょう。
(1)\(48\) (2) \(180\) (3) \(1001\)
(1)\(48 = 2^4 \times 3\)
(2)\(180 = 2^2\times 3^2 \times 5\)
(3)\(1001 = 7 \times 11 \times 13\)
(1)(2)の場合、\(2\)や\(3\)で割れそうだと容易に想像がつきます。
しかし、(3)の見当をつけるのは難しかったのではないでしょうか。
中には「えっ、\(1001\)って素数じゃないの!?」と思われた方もいるかもしれません。
「見つけるのは難しく、確かめるのは簡単」なことが素因数分解の性質といえるでしょう。
「1」が素数でない理由
仮に「1」が素数に含まれるとしましょう。
このとき、\(30\)を素因数分解するとどうなるでしょうか。

\[30 = 2\times 3\times 5\]
と表せるね!

いや、\(1\)も素数なんだから、
\[30 = 1\times 2\times 3\times 5\]
とした方がいいのかな…?

\(1\)って何回でもかけ算できちゃうよね!?
\[30 = 1\times 1 \times \cdots \times 1 \times 2\times 3\times 5\]
でもいいのかもしれない。混乱してきた…
このように「1」が素数に含まれていると、素因数分解の表し方が1通りに決まらず、いくつも出てきてしまいます。
これはとても不便なため、「1」を素数に含めないことにしているのです。
【補足】素因数分解の結果がただ1通りに表せることを「素因数分解の一意性」といいます。
まとめ
今回は「素数」や「素因数分解」について学習しました。
また、「1」が素数に含まれない理由も考えることができました。
この単元で学んだことは高校・大学数学に進んだ後にも出てくる非常に重要な概念です。
ただちに全てを理解する必要はないにしても、心のどこかに留めておいてもらえるとよいのかな、と思います。


