前回の記事では、加法と減法について学習しました。
今回は、乗法・除法(かけ算・わり算)について学習していきましょう。
結論
乗法・除法(かけ算・わり算)の計算で注意する点はたった1つです!
乗法・除法では、マイナス(\(-\))が2個あると打ち消しあってプラス(\(+\))となる
なぜそうなるの?と思った方は以下の説明を読んでみてください。
乗法(かけ算)の考え方
数直線上を歩く人を例に挙げて考えてみましょう。
\(3\)歩進む動作を\(3\)回行えば、合計で\(9\)歩進むこととなります。
このことを、\(3 \times 3 = 9\;\)と表します。

\(3 \times 2 = 6\;\)や\(\;3 \times 1 = 3\;\)の場合も同様です。
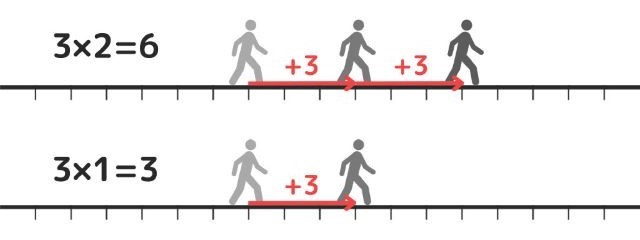
\(3 \times 0 = 0\;\)は、進む動作を\(0\)回行う(=一歩も進まない)という意味です。

それでは、かける数が\(-1,-2,\cdots\)となった場合はどうなるでしょうか。
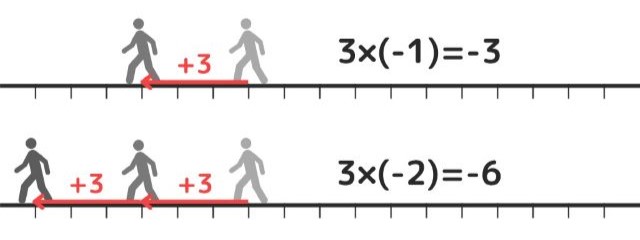
例えば、\(3\)歩進む動作を後ろを向いて\(2\)回行えば、合計で\(6\)歩戻ることとなります。
このことを、\(3 \times \)\((-2)\)\( = -6\;\)と表します。
【補足】
前回の記事で、引き算は「後ろを向く」ことに例えられることを説明しました。
すなわち「負の数をかける」ことは、「同じ数を連続で引き算する」ことを意味するのです。
他の例を見ていきましょう。

\(3\)歩下がる動作を\(2\)回行い、合計で\(6\)歩戻ることを、\((-3) \times 2 = -6\;\)と表します。

\(3\)歩下がる動作を後ろを向いて\(3\)回行い、合計で\(6\)歩進むことを、\((-3) \times\)\((-3)\)\(= 9\;\)と表します。
以上の例をルールとしてまとめてみましょう。
- 同符号のかけ算の答えは正(\(+\))
- 異符号のかけ算の答えは負(\(-\))
除法(わり算)の考え方
まず、わり算の考え方を復習しましょう。
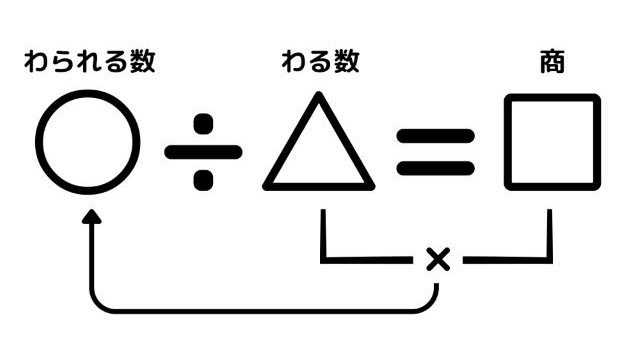
「商(わり算の答え)」と「わる数」をかけると、「わられる数」に戻ります。
わり算とは、このような条件を満たす商を求めることといえます。
例えば\(32\div 4\)の場合、「\(4\)とかけて\(32\)に戻る数は何?」と考えれば、\(4 \times 8 =32\)より答えは\(8\)となります。
この考え方は、わり算に負の数が含まれても同じように使うことが出来ます。
練習として以下の問題を解いてみましょう。
【問題】
(1)\(\;56 \div (-8)\)
(2)\(\;(-42)\div 3\)
(3)\(\;(-108)\div (-9)\)
(1)\(-7\)
\((-8)\times (-7)=56\)より、\(56 \div (-8) = -7\)となります。
(2)\(-14\)
\(3\times (-14)=42\)より、\((-42) \div 3 = -14\)となります。
(3)\(12\)
\((-9)\times 12=-108\)より、\((-108) \div (-9) = 12\)となります。
以上の計算をルールにまとめてみましょう。
- 同符号のわり算の答えは正(\(+\))
- 異符号のわり算の答えは負(\(-\))
3つ以上の数の乗法・除法
ここまでのルールをまとめます。
乗法・除法では、マイナス(\(-\))が2個あると打ち消しあってプラス(\(+\))となる
これを踏まえ、次の例を考えてみましょう。
\begin{align}
(-1)\times(-2)\times(-3)\times(-4)&=2\times (-3) \times (-4)\\
&= (-6)\times (-4)\\
&=24
\end{align}
計算の途中で、マイナス(\(-\))同士が打ち消しあっています。
3つ以上の数になっても、前から順番に計算していけば答えを得られるのです。
練習として以下の問題を解いてみましょう。
【問題】
(1)\(\; (-3)\times (-4) \times (-5)\)
(2)\(\; 12\div (-3) \times 9\)
(3)\(\displaystyle \; (-6)\times \left(-\frac{3}{5}\right)\times 15 \div 9\)
(1)\(-60\)
\[ (-3)\times (-4) \times (-5) = 12 \times (-5) = -60\]
3個のマイナスのうち2個が打ち消しあい1個が残るため、答えの符号はマイナスとなります。
(2)\(-36\)
\[12\div (-3) \times 9 = -4 \times 9 = -36\]
(3)\(6\)
\[\; (-6)\times \left(-\frac{3}{5}\right)\times 15 \div 9 = \frac{6\times 3 \times 15}{5 \times 9}=6\]
2個のマイナスが打ち消しあい、答えの符号はプラスとなります。
まとめ
前回(加法と減法)に引き続き、乗法と除法も慣れが肝心です。
たくさん計算練習をして、スムーズに計算できるようにしましょう!


