小学算数と中学数学で最大の違いは「負の数」の登場にあるといってもよいでしょう。
この記事では、「負の数」の考え方について説明していきます。

これから一緒に頑張っていきましょう!
身近な「負の数」
\(0\)よりも大きい数のことを「正の数」、\(0\)よりも小さい数のことを「負の数」といいます。
※0は正の数でも負の数でもありません。
\(0\)より小さいってどういうこと?と思われるかもしれませんが、実は日常生活で広く使われているものでもあります。
たとえば今日の気温が「マイナス3度」と言われた場合は、0度よりも3度低い気温であるという意味です。


ほかにも身近な例がないか、考えてみよう。
数直線で考える
次の図のように、道路に人が立っています。
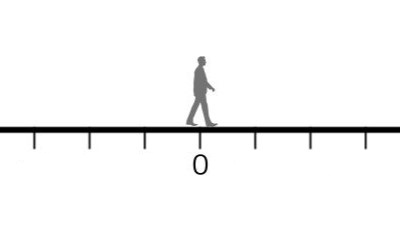
はじめに立っている位置を\(0\)としましょう。
この人が前に1歩進んだ位置を「\(+1\)(プラス1)」と表すことにします。
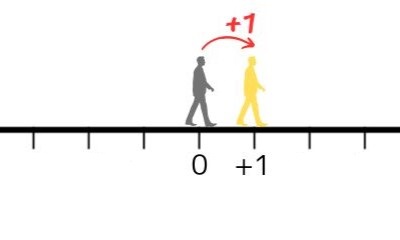
同様に、2歩進んだら「\(+2\)」、3歩進んだら「\(+3\)」、…といったように表せます。
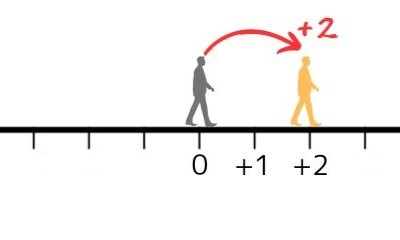
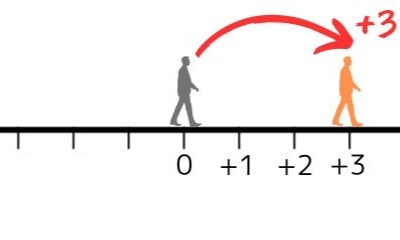
そして、この人が後ろに1歩下がった位置を「\(-1\)(マイナス1)」と表します。
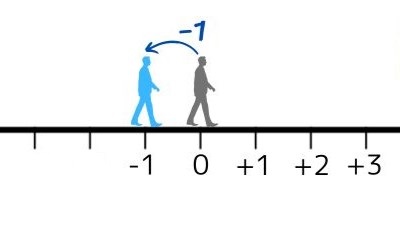
この「\(-1\)」は負の数のひとつです。
負の数とは、\(0\)よりも小さい数のことをいいます。
ここでは、はじめの位置(\(0\))よりも後ろであるという状況を「\(-\)」という符号で表しているのです。
同様に、2歩下がったら「\(-2\)」、3歩下がったら「\(-3\)」、…といったように表せます。
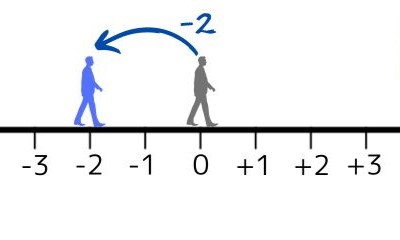

このように数を埋めていくと、次のような「直線に数字が順番に書かれた図」ができあがります。
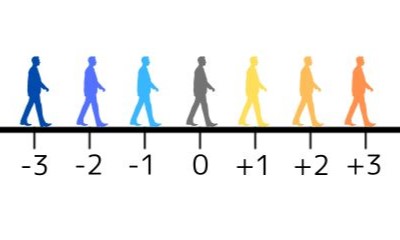
これを「数直線」とよびます。
絶対値 = 歩数!
上の例で、前に1歩進んだら「\(+1\)」、後ろに1歩下がったら「\(-1\)」と表せると分かりました。
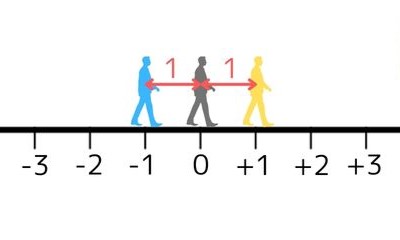
ところで、前に1歩進んでも後ろに1歩下がっても、はじめの位置から「\(1\)」歩分離れたことは同じことです。
このように、はじめの位置からどれだけ離れたかを表す数を「絶対値」とよびます。
絶対値を表すときは、符号(\(+\)や\(-\))を付けずに数字だけ書くきまりとなっています。
例えば、\(+7\)の絶対値は「\(7\)」と書き、\(-8\)の絶対値は「\(8\)」と書きます。
まとめ
今回は負の数について学習しました。
数直線を上手く活用して、「0より小さい数」への理解を深めていきましょう。
- 正の数\(\rightarrow\)\(0\)より大きい数のこと
- 負の数\(\rightarrow\)\(0\)より小さい数のこと
- 絶対値\(\rightarrow\)\(0\)からどれだけ離れているかを表す数で、符号を付けずに書く


